Basic Mathematics Formulas for All Exams

Basic Mathematics Formula for NDA, CGL, Bank Exams, CTET, SSC, UPSC, ISRO, ONGC, Group-C Exams, Banks, PO, MBA, MAT, CAT, Railways etc.

Basic Mathematics Formulas for All Exams

Mathematics is an essential section for most competitive exams, such as the SSC, UPSC, CAT, and banking exams. It typically accounts for 1/3 to 1/4 of the total marks, so it is important to have a strong foundation in the subject. In addition to having a strong understanding of the concepts, it is also important to be able to solve problems quickly and accurately. This can be achieved through practice and by learning shortcuts and tricks. With these formulas, hard work and dedication, you can master the mathematics section of any competitive exam.

Areas of Basic Geometrical Shapes

Area of a triangle = 1/2 × base × height
Heron’s formula: This formula is the most general formula for the area of a triangle, and it can be used for any triangle, regardless of its shape. The formula is: K = √[s(s – a)(s – b)(s – c)], where K is the area of the triangle, s is the semi perimeter of the triangle, which is equal to (a + b + c)/2 , and a, b, and c are the side lengths of the triangle.
Area of a square = side² or Side × Side
Area of a rectangle = length × breadth
Area of a circle = πr², where π = 22/7 and r is the radius of the circle
Area of a parallelogram = base × height
Area of a trapezium = 1/2 × (sum of parallel sides) × (perpendicular distance between them)
Area of a rhombus = 1/2 × d1 × d2, where d1 and d2 are the diagonals of the rhombus
Area of an equilateral triangle = √3/4 × side²
Area of an isosceles triangle = 1/2 × (base × height)
Area of a circle sector = (1/2 × θ × πr²), where θ is the angle subtended by the sector at the centre of the circle
Area of a circular segment = (1/2 × (θ – π/2) × πr²), where θ is the angle subtended by the segment at the centre of the circle

Volume of Basic Geometrical Shapes

Volume of Cube = a³, where a is the side of the cube.
Volume of Cuboid = l × b × h, where l is the length, b is the breadth, and h is the height of the cuboid.
Volume of Pyramid = (1/3) × B × h, where B is the area of the base of the pyramid and h is the height of the pyramid.
Volume of Rectangular Prism = l × b × h, where l is the length, b is the breadth, and h is the height of the rectangular prism.
Volume of Sphere = (4/3)πr³, where r is the radius of the sphere.
Volume of Cylinder = πr²h, where r is the radius of the base of the cylinder and h is the height of the cylinder.
Volume of Cone = (1/3)πr²h, where r is the radius of the base of the cone and h is the height of the cone.

Surface Area of Basic Geometrical Shapes

Total Surface Area of Cuboidal Box = 2(lb + bh + hl)
Surface Area of Cabinet = lb + 2(bh + hl)
Surface Area of Cube = 6l²
Surface Area of Cylinder = 2πr (h + r)
Lateral Surface Area of Cylinder = 2πrh
Lateral Surface Area of Cube = 4l²
Curve Surface Area of Hollow Cylinder = 2πrh
Surface area of a sphere = 4πr², where “r” is the radius of the sphere.
Surface area of a cone = πr(l + r), where “r” is the radius of the cone, “l” is the slant height of the cone, and “π” is a mathematical constant approximately equal to 3.14.

Perimeter of Basic Geometrical Shapes

Perimeter of rectangle = 2(l + b), where l is the length and b is the breadth of the rectangle.
Perimeter of square = 4(s), where s is the side length of the square.
Perimeter of circle = 2πr, where π (pi) is a mathematical constant approximately equal to 3.14 and r is the radius of the circle.
Perimeter of triangle = a + b + c, where a, b, and c are the side lengths of the triangle.
Perimeter of trapezoid = a + b + c + d, where a, b, c, and d are the side lengths of the trapezoid.
Perimeter of parallelogram = 2(a + b), where a and b are the side lengths of the parallelogram.
Perimeter of rhombus = 4(s), where s is the side length of the rhombus.
Perimeter of pentagon = a + b + c + d + e, where a, b, c, d, and e are the side lengths of the pentagon.
Perimeter of a regular pentagon = 5 × side, The all sides of regular pentagon are equal.
Perimeter of hexagon = a + b + c + d + e + f, where a, b, c, d, e, and f are the side lengths of the hexagon.
Perimeter of a regular hexagon = 6 × side, The all sides of regular hexagon are equal.
Perimeter of a regular octagon = 8 × side, The all sides of regular octagon are equal.

Profit = Selling price – Cost price
Loss = Cost price – Selling price
Profit percent = (Profit / Revenue) × 100%
Loss percent = (Loss / Revenue) × 100%
Markup = Selling price – Cost price. (Markup is the amount of money that a business adds to the cost price of a product or service to get a selling price.)
Markdown = Cost price – Selling price. (Markdown is the amount of money that a business subtracts from the selling price of a product or service to get a cost price.)
Profit margin = (Profit / Revenue) × 100 (Profit margin is a measure of how profitable a business is. It is calculated by dividing the profit by the revenue and multiplying by 100%.)
Return On Investment (ROI) = (Profit / Investment) × 100% (ROI is a measure of how much profit a business makes for every dollar that it invests.)
Break-even point = Fixed costs / Contribution margin. (The break-even point is the point at which a business makes no profit and no loss.)
Cost price = Direct costs + Indirect costs (Cost price is the amount of money that a business pays to produce or acquire a product or service.)
Selling price = Cost price + Profit. (Selling price is the amount of money that a business charges for a product or service.)

Speed, Distance and Time Formulas

Speed = Distance / Time
Distance = Speed × Time
Time = Distance / Speed
Average speed = Total distance / Total time
Instantaneous speed = Change in distance / Change in time

Percentage = (part / whole) × 100
Percentage change = (new value – old value) / old value × 100
Percentage increase = (new value – old value) / old value × 100
Fraction = percentage / 100
Decimal = percentage / 100.

Banking Formula

Simple interest = (Principal × Rate × Time)/100
Amount = Principal + Simple interest

Surds and Indices

Laws of Indices

a^m aⁿ= a^m+n
a^m aⁿ= a^m-n
(a^m)ⁿ= a^mn
(ab)ⁿ= aⁿ+ bⁿ
a⁰ = 1

Laws of Surds

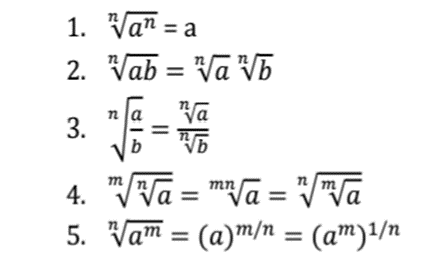
Compound Proportion

Chain Rule: (a:b)::(c:x) => (a × x) = (b × c)

or x = (b × c)/a

Pipe and Cisterns

If a pipe can fill a tank in x hours, then the part filled in 1 hr = 1/x.
If a pipe can empty a tank in y hours, then the part emptied in 1 hr = 1/y.
If a pipe can fill a tank in x hours and another pipe can empty the same tank in y hours, then the net part filled in 1 hr, when both the pipes are opened = (xy)/(y – x), provided y > x.
If a pipe can fill a tank in x hours and another can fill the same tank in y hrs, then the net part filled in 1 hr, when both the pipes are opened = (x + y)/(xy), provided xy > 0.
If two pipes take x and y hours respectively to fill a tank of water and a third pipe is opened which takes z hours to empty the tank, then the time taken to fill the tank = {1 / (1/x)+(1/y)+(1/z)} and the net part filled in 1 hr = (1/x)+(1/y)-(1/z).
A pipe can fill a tank in a hrs. Due to a leak in the bottom it is filled in b hrs. If the tank is full, the time taken by the leak to empty the tank = ab/(b – a) hrs.

Diameter: The diameter of a circle is the distance across the circle, passing through the center. The diameter is twice the radius.
- Formula: D = 2r
Radius: The radius of a circle is the distance from the center of the circle to any point on the circle.
- Formula: r = d/2
Circumference: The circumference of a circle is the distance around the circle.
- Formula: C = 2πr
Area: The area of a circle is the amount of space enclosed by the circle.
- Formula: A = πr²
Semicircle: A semicircle is half of a circle. It has a diameter, a radius, a circumference, and an area.
- Formula for semicircle circumference: C = πr + 2r
- Formula for semicircle area: A = πr²/2

Radius: The radius of a sphere is the distance from the center of the sphere to any point on the surface of the sphere.
- Formula: r = d/2
Diameter: The diameter of a sphere is the distance across the sphere, passing through the center. The diameter is twice the radius.
- Formula: d = 2r
Volume: The volume of a sphere is the amount of space enclosed by the sphere.
- Formula: V = (4/3)πr³
Surface area: The surface area of a sphere is the total area of the surface of the sphere.
- Formula: A = 4πr²

Formulas for Cone

Volume: The volume of a cone is the amount of space enclosed by the cone.
- Formula: V = (1/3) 4πr²h
Curved surface area: The curved surface area of a cone is the area of the lateral surface of the cone.
- Formula: CSA = πrl
Total surface area: The total surface area of a cone is the sum of the curved surface area and the area of the base.
- Formula: TSA = πrl + 4πr²

Formulas for frustum of a cone

The volume of a frustum of a cone = V = (1/3)π[(R² + r² + Rr)h], where V is the volume of the frustum, R is the radius of the larger base, r is the radius of the smaller base, and h is the slant height of the frustum.
Lateral Surface Area frustum of a cone = π(R + r)√((R – r)^2 + h^2)
Total Surface Area of a frustum of a cone = Lateral Surface Area + πR² + πr²

Algebra Formulas

(a+b)²= a² +b² + 2ab
(a-b)²= a² +b² – 2ab
(a+b)²– (a-b)² = 4ab
(a+b)²+ (a-b)² = 2(a² + b²)
(a+b+c)²= a² + b² + c² + 2(ab + bc + ca)
(a² – b²) = (a+b) (a-b)
(a+b)³= a³ + b³ + 3ab + (a + b)
(a-b)³= a³ – b³ – 3ab + (a – b)
(a³ + b³) = (a+b) (a² + b² – ab)
(a³ – b³) = (a-b) (a² + b² + ab)
(a³ + b³+ c³-3abc) = (a+b+c) (a² + b² + + c³ -ab-bc-ca)
a + b + c = 0 => a³ + b³+ c³ = 3abc

Clock Points to Remember

The angle formed by the hour needle in one hour = 30 degree
The angle formed by the minute needle in 5 minutes = 30 degree
The distance covered by a hour needle in 1 hour = 5 minutes distance
The distance covered by a minute needle in 1 minute = 1 minutes distance
The extra distance covered by a minute needle than hour needle in 1 hour = 55 minutes distance
When minute and hour needles at 90 degree then they are at 15 minutes distance. This happened twice in every hour.

CTET Exam 2023: Exam Date, Paper Format and Eligibility

Career Options after Graduation in 2023: Exploring the Pathways to Success

How to Score Full Marks in Exams: 6 Proven Strategies

Spread the love